作成者: @fujidig, 作成日: 2020/4/14
Moschovakisの"Descriptive Set Theory" (2009)の1E節のExercisesの解答です.
$f: \mathcal{X} \to \mathcal{Y}$が連続なら \[ \Graph(f) = \{ (x, y) : f(x) = y \} \] が閉集合なことを示せ.
$\Delta = \{ (y, y) : y \in \mathcal{Y} \}$は$\mathcal{Y} \times \mathcal{Y}$の閉集合である ($\mathcal{Y}$のHausdorff性). 今,この集合$\Delta$を$f \times \mathrm{id}: \mathcal{X} \times \mathcal{Y} \to \mathcal{Y} \times \mathcal{Y}; (x, y) \mapsto (f(x), y)$で引き戻せば,$\Graph(f)$が得られる. よって,$f \times \mathrm{id}$は連続なことから,$\Graph(f)$は閉集合である. □
$f: \mathcal{X} \to \mathcal{Y}$が連続かつ$P$が$\mathcal{X}$の$\boldsig^1_n$部分集合ならば, \[ f[P] = \{f(x) : P(x)\} \] も$\boldsig^1_n$である.
$\Graph(f) \cap (P\times\mathcal{Y})$を$\mathcal{Y}$に射影したものが$f[P]$である. Exercise 1E.4より$\Graph(f)$は閉集合で$P \times \mathcal{Y}$は$\boldsig^1_n$なので$\Graph(f) \cap (P\times\mathcal{Y})$は$\boldsig^1_n$. よってその射影$f[P]$も$\boldsig^1_n$である. □
任意の集合$P \subset \mathcal{X}$について, \begin{align*} \text{$P$が$\boldsig^1_1$} &\iff \text{$P = f[\mathcal{N}]$ for some continuous $f$} \\ \text{$P$が$\boldsig^1_{n+1}$} &\iff \text{$P = f[Q]$ for some $\boldpi^1_n$ set $Q \subset \mathcal{N}$ and some continuous $f$} \end{align*} を示せ.
$P$を$\boldsig^1_1$集合とすると,ある閉集合$C \subset \mathcal{X} \times \mathcal{N}$があって$P = \exists^\mathcal{N} C$である. $C$はポーランド空間の閉集合なので再びポーランド空間である.よって,連続全射$\pi: \mathcal{N} \to C$が存在する.$\pi$と射影$\mathcal{X} \times \mathcal{N} \to \mathcal{X}$の合成が求めていた関数である.
$P$を$\boldsig^1_{n+1}$集合とする. すると$P = \exists^\mathcal{N} Q$で$Q \subset \mathcal{X} \times \mathcal{N}$で$Q$は$\boldpi^1_n$となる. $\mathcal{X} \times \mathcal{N}$から$\mathcal{X}$への射影を$p$とする. 連続全射$\pi: \mathcal{N} \to \mathcal{X}$をとる. また,同相写像$i: \mathcal{N} \to \mathcal{N} \times \mathcal{N}$をとる. このとき$p \circ (\pi \times \mathrm{id}) \circ i$と$i^{-1}((\pi \times \mathrm{id})^{-1}(Q))$が求めるべき写像と集合である. □
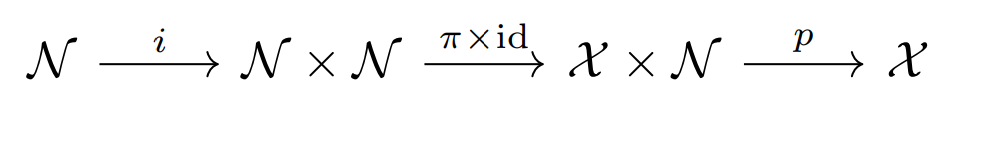
$f: \R \to \mathcal{X}$が連続かつ$F \subset \R$が閉集合なら,$f[F]$は$\boldsig^0_2$である.
$\R$は$\sigma$コンパクトなので,閉集合$F$はコンパクト集合の可算和で書ける: \[ F = \bigcup_{i \in \omega} K_i \] ここに各$K_i$はコンパクト集合.すると \[ f[F] = f[\bigcup_{i \in \omega} K_i] = \bigcup_{i \in \omega} f[K_i]. \] コンパクト集合の連続写像による像はコンパクトなので,各$f[K_i]$はコンパクトである.よって,$f[F]$は閉集合の可算和で表されるので,$\boldsig^0_2$である. □
空間$C[0, 1]$において \begin{align*} Q(f) &\iff \text{$f$は$[0,1]$上微分可能} \\ R(f) &\iff \text{$f$は$[0,1]$上連続微分可能} \end{align*} とおく.$Q$が$\boldpi^1_1$で$R$が$\boldsig^1_1$なことを示せ.
$S \subset C[0, 1] \times [0, 1]$を \[ S(f, x) \iff \text{$f$は点$x$で微分可能} \] とおくと,$S$は$\boldpi^0_3$である (問題1C.4を参照). そこで \[ Q(f) \iff \forall x \in [0, 1], S(f, x) \] は$\boldsig^1_1$である. $F: C[0, 1] \to C[0, 1]$を \[ F(f)(x) = \int_0^x f(x) dx \] とおくと$F$は連続である.よって, \[ R(f) \iff \exists g \in C[0, 1], \exists a \in \R, f = F(g) + a \] により,$R$は$\boldsig^1_1$である. 実際は$R$はもっと複雑さが低く,$\boldpi^0_3$になる.Anush Tserunyanの講義ノートを参照せよ.
参考: